Does basic cybernetics prove that estimating our methane emissions is impossible?

[teo123]

I've come across a new argument against mainstream climate science, and it makes some degree of sense to me. It's about applying the math we were taught in our Control Engineering classes to climate.
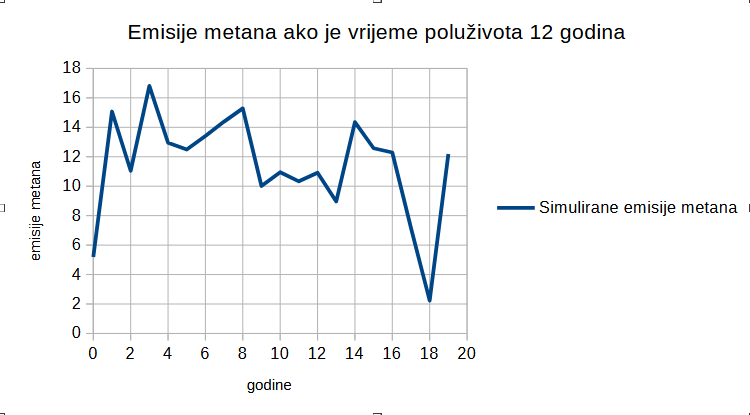
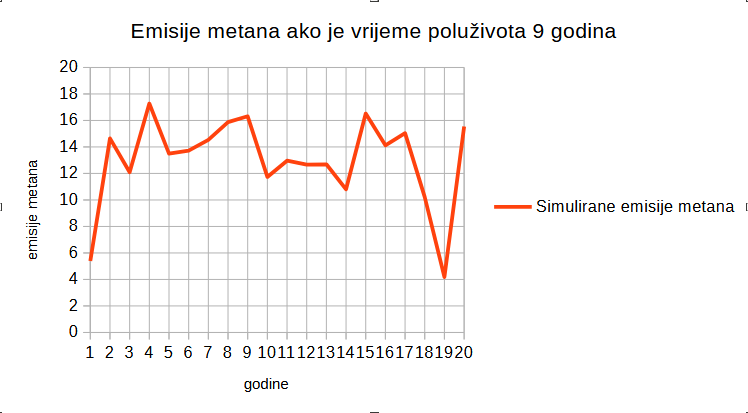
We've all seen this type of diagrams, right?

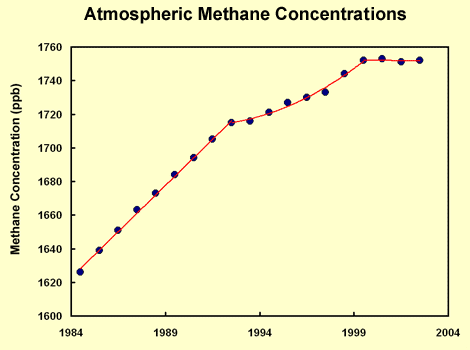
The argument goes that our methane emissions must be approximately equal to the derivative of that curve, slightly larger than that because methane in the atmosphere has a half-life of 12 years (that it would equal to the derivative if the half-life was infinite, but actually it is slightly larger than that). So it is visible from the diagram that our methane emissions reached their peak somewhen in 1980s and have been decreasing ever since. Makes sense, right? Well, according to this new argument I found, that's actually not the right inference, but the right inference is that our methane emissions have been approximately constant. That would be the right inference if methane in the atmosphere were a IT1-type system, but it actually isn't.
To understand why, try to derive the transfer function. Now, it might not be obvious how to derive the transfer function directly (or even how to set up the differential equations), but ask yourself: What is the impulse response (the response to the Dirac delta function)? It seems obvious that it is approximately:
g(t)=e^(ln(2)/12*t)
And since for linear time-invariant systems (which methane in the atmosphere approximately is) the transfer function is equal to the Laplace transform of the impulse response, that means the transfer function has to be:

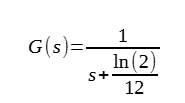
So, what is its step-response? How would a system described by that transfer function respond to constant methane emissions? Well, type this into Octave or MatLab:

Code: Select all

pkg load control;
s=tf('s');
step(1/(s+log(2)/12))

It outputs this:

Which looks like the diagram of methane concentration in the atmosphere over time.
Does this curve converge or does it go to infinity. Well, that be determined using the final value theorem of the Laplace transform. The Laplace transform of the step response is, of course:
S(s)=1/s*G(s)
And the limit of the step response as time approaches infinity is, by the final value theorem:
lim(t -> inf, s(t))=lim(s->0,s*S(t))=12/ln(2)
So, given that, according to the diagram, the amount of methane in the atmosphere rose from 1620 to 1760. Therefore, our methane emissions are:
(1760-1620)/(12/ln(2))=8.0867
And they are constant.
What do you think is wrong with that argument?
I e-mailed my Control Engineering professor [redacted] about it to see what he thinks.

[teo123]

@Red, you are a civil engineer, right? Have you taken any Control Theory classes? If so, what do you think about that argument?

[teo123]

My control engineering professor responded to my e-mail, but he essentially said "I don't know.". I haven't received his permission to post his response onto an Internet forum, and, even if I did, that wouldn't really advance the conversation.

@brimstoneSalad, you said elsewhere that you had taken some aerospace engineering classes at a university, right? Have you taken any control engineering classes? If so, what do you think, does basic control engineering prove that our methane emissions are not approximately proportional to the first derivative of the concentration of methane in the atmosphere? That it would be true if concentration of methane in the atmosphere were an IT1-type system, but that it isn't.

[teo123]

Anyway, here is what my Control Engineering professor has to say:

Kolega Samaržija,

teško da ćemo na ovaj način doći do rješenja koje tražite jer ja ne poznam ovaj proces. To je kemijski proces koji ne poznajem, niti znam na koje se sve načine metan generira, kako dolazi u atmosferu, gdje se i u kojim oblicima zadržava, s kojim drugim strukturama se veže i modificira, kojom brzinom se razgrađuje u atmosferi, … Sve te mehanizme treba poznavati kako bi se mogla modelirati količina metana u atmosferi. Teško da bi u toj procjeni mogla pomoći i mjerenja u pojedinim točkama atmosfere jer je to ogromno područje, vrlo složenog kemijskog sastava, velikih strujanja zračnih masa, … O tim stvarima pokušajte više saznati iz nekih internetskih izvora. Možda naiđete i na neke modele (matematičke opise) koji vam mogu pomoći u rješavanju ovog problema.

Pozdrav

He asked me not to post his name. However, I already included it in the OP, and I cannot edit it out. Can somebody please do that for me?

[brimstoneSalad]

You're overthinking this Teo, as usual. You should stop wasting your time looking for arguments against mainstream climate science, you're too vulnerable to pseudoscience to evaluate them.

We've been outputting a lot of methane for a long time due to widespread animal agriculture, oil drilling, and landfills. The first has gotten a bit worse while the latter two have probably improved nominally. I'd have to spend a lot of time researching to give some kind of quantity guess.
I don't see what you think any of that has to do with mainstream climate science though. Methane is a potent greenhouse gas wherever it comes from, and because it has a short half-life we should limit it as much as possible and see returns quickly.

It's really hard to track emissions because they're basically leaks in the latter two cases and there are a so many variables that effect production from landfills. Open wells are also big unknowns in terms of how much they'll supply for how long. Animal ag. is a little more predictable as sources go, but it's not the only anthropogenic one.

[teo123]

You're overthinking this Teo, as usual.

What do you mean by "overthinking"?

You should stop wasting your time looking for arguments against mainstream climate science, you're too vulnerable to pseudoscience to evaluate them.

Well, now I am no longer a high-school student, I am an engineer, so I am not supposed to be as vulnerable to pseudoscience as I used to be.

The first has gotten a bit worse

I... that... How can you say something like that? There are fewer cows around the world now than there were a few decades ago, and those cows that we do have are predominantly grain-fed, rather than grass-fed as they were a few decades ago.

[teo123]

I've made a YouTube video about this problem: https://youtu.be/EWI3wIJTZXg

[brimstoneSalad]

You should stop wasting your time looking for arguments against mainstream climate science, you're too vulnerable to pseudoscience to evaluate them.

Well, now I am no longer a high-school student, I am an engineer, so I am not supposed to be as vulnerable to pseudoscience as I used to be.

I think it has more to do with your particular psychology.

The first has gotten a bit worse

I... that... How can you say something like that? There are fewer cows around the world now than there were a few decades ago, and those cows that we do have are predominantly grain-fed, rather than grass-fed as they were a few decades ago.

There has been a recent downtrend in beef consumption in the U.S. since it's peak around 1980-ish. I don't know what all countries that holds for, I'm not doing a research project for you Teo. Globally my understanding is that it's still rising and projected to continue doing so. China is a major player in that.
More cows more methane.

Also, grain feeding is not new. It's been done for hundreds of years, whether over-wintering or for finishing. The large feedlots started finishing cows on grain in a big way in the 50's. That's when it started taking over as the dominant practice and beef demand exploded. Incidentally it's probably part of WHY demand exploded.

Regardless, grain feeding is not a panacea. It's still very bad. Faster finishing times only result in small reductions.

Teo, you're almost always wrong about almost everything. Stop trying to be novel and thinking you can spot the errors of professionals. I've told you so many time, you're too conspiratorial and too ready to jump to conclusions. It wastes everybody's time. That's why people ignore you.

[teo123]

More cows more methane.

Correct, but now we are able to produce more meat with fewer cows. The changes in genetics of cows and the changes in diet of cows make that possible.

Regardless, grain feeding is not a panacea.

But the problem is that many vegans are claiming that grass-fed cows emit around 3 times as much methane per a litre of milk than grain-fed cows.

Stop trying to be novel and thinking you can spot the errors of professionals.

Look, it's important to listen to experts. But it's even more important to be able to detect situations when the experts are not actually saying what the politicians and activists are saying that they are saying. Are the experts actually saying that our methane emissions reached their peak in the 1980s and have been decreasing ever since? Or is it just a statistically flawed analysis of the data, and not the actual scientific consensus? Are the experts actually saying that grass-fed cows emit 300% as much methane as the grain-fed cows? Or do they say it is probably around 20%?

I've told you so many time, you're too conspiratorial and too ready to jump to conclusions.

And it's not me who noticed the problem, it's the Quora user called Malcolm Forster who informed me of the problem.

[teo123]

Do you think this JavaScript program will correctly estimate our methane emissions? It uses the Gaussian method to approximate them and then uses a genetic algorithm to try to improve the approximation.

Code: Select all

const koncentracije_metana_ocitane_s_grafa = [
  1625, 1640, 1650, 1665, 1675, 1685, 1695, 1705, 1715, 1720,
  1725, 1730, 1735, 1737, 1745, 1750, 1755, 1755, 1750, 1755
];
const krivulja =
    koncentracije_metana_ocitane_s_grafa.map((x) => { return x - 1620; });
const vrijeme_poluzivota_metana = 12; // Procjene se kreću između 9 i 12.
let jedinke = [];
const koliko_jedinki_imamo = 12;
function nasumicno_generiraj_pokusaj() {
  const niz = [];
  let trenutni = 2 * (1760 - 1600) / (vrijeme_poluzivota_metana / Math.log(2)) *
                 Math.random();
  while (niz.length < krivulja.length) {
    niz.push(trenutni);
    trenutni += Math.random() * 3 - 3 / 2;
  }
  return niz;
}
function aproksimiraj_Gaussovom_metodom() {
  const niz = [];
  for (let i = 0; i < krivulja.length; i++) {
    let razlika = krivulja[i];
    for (let j = 1; j <= i; j++)
      razlika -= niz[i - j] * Math.E **
                 (Math.log(1 / 2) / vrijeme_poluzivota_metana * j);
    razlika += Math.random() - 1 / 2;
    niz.push(razlika);
  }
  return niz;
}
jedinke.push(aproksimiraj_Gaussovom_metodom());
while (jedinke.length < koliko_jedinki_imamo ** 2)
  jedinke.push(nasumicno_generiraj_pokusaj());
function koncentracija_metana_u_atmosferi(emisije_metana_po_godinama) {
  const koncentracija_metana_u_atmosferi = [];
  for (let i = 0; i < emisije_metana_po_godinama.length; i++) {
    let zbroj = 0;
    for (let j = 0; j <= i; j++)
      zbroj += emisije_metana_po_godinama[i - j] * Math.E **
               (Math.log(1 / 2) / vrijeme_poluzivota_metana * j);
    koncentracija_metana_u_atmosferi.push(zbroj);
  }
  return koncentracija_metana_u_atmosferi;
}
function izracunaj_gresku(koncentracije_metana_u_atmosferi) {
  let zbroj = 0;
  if (krivulja.length != koncentracije_metana_u_atmosferi.length)
    throw "Neki dio programa je promijenio velicinu niza, prekidamo!";
  for (let i = 0; i < krivulja.length; i++)
    zbroj += (krivulja[i] - koncentracije_metana_u_atmosferi[i]) ** 2;
  return zbroj;
}
function krizaj_dva_pokusaja(prvi, drugi) {
  if (prvi.length != drugi.length)
    throw "Neki dio programa je promijenio velicinu niza, prekidamo!";
  const novi_niz = [];
  if (Math.random() < 1 / 2) {
    novi_niz.push((prvi[0] + drugi[0]) / 2);
    let trenutni = novi_niz[0];
    for (let i = 1; i < prvi.length; i++)
      if (Math.random() < 1 / 2) {
        trenutni += prvi[i] - prvi[i - 1];
        novi_niz.push(trenutni);
      } else {
        trenutni += drugi[i] - drugi[i - 1];
        novi_niz.push(trenutni);
      }
  } else {
    for (let i = 0; i < prvi.length; i++)
      if (Math.random() < 1 / 2)
        novi_niz.push(prvi[i]);
      else
        novi_niz.push(drugi[i]);
  }
  return novi_niz;
}
function nasumice_izmijeni(pokusaj) {
  const novi_pokusaj =
      pokusaj.map((x) => { return x + Math.random() * 3 - 3 / 2; });
  return novi_pokusaj;
}
function sortiraj_jedinke_i_zadrzi_najbolje() {
  jedinke.sort((prva, druga) => {
    return izracunaj_gresku(koncentracija_metana_u_atmosferi(prva)) <
           izracunaj_gresku(koncentracija_metana_u_atmosferi(druga));
  });
  jedinke = jedinke.slice(0, koliko_jedinki_imamo);
}
let brojac = 0;
while (brojac < 1_000) {
  sortiraj_jedinke_i_zadrzi_najbolje();
  for (let i = 0; i < koliko_jedinki_imamo; i++) {
    for (let j = 0; j < koliko_jedinki_imamo; j++) {
      if (i == j)
        continue;
      if (Math.random() < 1 / koliko_jedinki_imamo)
        jedinke.push(
            nasumice_izmijeni(krizaj_dva_pokusaja(jedinke[i], jedinke[j])));
      else
        jedinke.push(krizaj_dva_pokusaja(jedinke[i], jedinke[j]));
    }
    jedinke.push(nasumice_izmijeni(jedinke[0]));
    jedinke.push(
        nasumicno_generiraj_pokusaj()); // Biološki krajnje nerealistično
                                        // (abiogeneza se ne događa danas), ali
                                        // izgleda da program daje bolje
                                        // rezultate ovako.
  }
  for (let i = 0; i < 6; i++) // Dakle, neka najbolja jedinka ima 6+1=7 djece sa
                              // svakom drugom jedinkom.
    for (let j = 1; j < koliko_jedinki_imamo; j++)
      jedinke.push(krizaj_dva_pokusaja(jedinke[0], jedinke[j]));
  brojac++;
}
sortiraj_jedinke_i_zadrzi_najbolje();
const izlaz_simulacije = koncentracija_metana_u_atmosferi(jedinke[0]);
console.log(
    "Godine\tSimulirane emisije metana\tSimulirana koncentracija metana");
for (let i = 0; i < jedinke[0].length; i++)
  console.log(i + "\t" + jedinke[0][i] + "\t" + izlaz_simulacije[i]);
console.log(
    "Ukupno kvadratno odstupanje simulirane koncentracije metana od mjerenih podataka: " +
    izracunaj_gresku(izlaz_simulacije));

Here is what it outputs if you set it that the half-life of methane is 12 years:

Here is what it outputs if you set it that the half-life of methane is 9 years:


[EDIT: Updated image here on request of poster: http://philosophicalvegan.com/viewtopi ... 644#p52644 ]
Either way, there doesn't seem to be a clear upward or a downward trend here. What strikes me as weird is that the 9th year is a peak if you assume the half-life is 12, but it's a valley if you assume the half-life is 9. I don't know how that's possible. Can somebody explain that to me?